15パズルの解き方
15パズルは、1874年にノイス・チャップマン(Noyes Palmer Chapman)が考案したGem Puzzle が原案となっていますが、
1878年にサム・ロイドが1000ドルの懸賞金かけて出題したいわゆる「14-15パズル」で中毒者が出るほど有名になりました。
15パズルのゴールは図1に示す通りですが、サム・ロイドが出題したいわゆる「14-15パズル」とは、図1の14と15のパネルを入れ替えた状態から、図1のゴールへ導くという問題です。
どうでしょう、一見、「簡単かも知れない」と思う方もいらっしゃるかも知れませんが、実は、これは解くことが不可能な問題なのです。

図1 15パズルのゴール
14-15パズルが解けないことの証明
15パズルのは論理力を鍛えるためのスマホゲームですので、簡単な数学を使用してわかりやすく解説しましょう。
それ程難しい数学を使う訳ではありませんので、数学が苦手な方でもこのページをしっかり読めば理解できるでしょう。
パネルを1次元配列で表現
まず、15パズルでパネルを動かした時、何が起こっているのかを数学的かつ論理的に解釈するため、パネル配置を1次元配列で表します。
1次元配列といっても難しく考える必要はありません。単に、左上のパネルの数字から右横に読み進め、右端まで来たら次の行の左端から同様に読んで行って並べるだけです。
例えば、図1に示すゴールの状態を1次元配列Gで表すと次のようになります。ここで、「空」は空白、即ちパネルが無い場所を表します。
G = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,空}
パネルを動かした時の1次元配列の変化
次に、パネルを動かした時に、この1次元配列がどのように変化するのかを見てみましょう。
図2~図5の状態A~状態Dを1次元配列A,B,C,Dで表せば次のようになります。
A = {12,10,8,空,7,2,3,9,1,11,15,6,4,14,5,13}
B = {12,10,8,9,7,2,3,空,1,11,15,6,4,14,5,13}
C = {12,10,8,9,7,2,空,3,1,11,15,6,4,14,5,13}
D = {12,10,空,9,7,2,8,3,1,11,15,6,4,14,5,13}

図2 15パズルのある状態A

図3 状態Aからパネル9を上に移動(状態B)

図4 状態Bからパネル3を右に移動(状態C)

図5 状態Cからパネル8を下に移動(状態D)
このパネル操作と1次元配列の変化との関係から、以下のことがわかります。
- パネル動かすということは、「空」と動かしたパネル数字との入れ替えである。
- パネルを横に動かす操作は、「空」と横のパネル数字との入れ替えである。
- パネルを縦に動かす操作は、「空」と4つ右または左のパネル数字との入れ替えである。
ここで、重要なことは、パネルを1コマ動かすという動作は、「空」とパネル数字の入れ替え、即ち1回の「置換」で表現できるということです。
さらに、パネルを1コマ動かすことにより「空」も一コマ動きます。
以上から、『「空」とパネルの置換回数と「空」を動かす回数を加えると偶数になる』という重要な法則が導き出せます。
3x3の8パネルや5x5の24パネル問題においても、パネルを縦に動かした時に、8パネルでは3つ右または左に動き、24パネルでは5つ右または左に動く点が異なるだけで、法則は同じです。
14-15パズルが解けないことの証明
ここまで理解すれば、サム・ロイドが出題した「14-15パズル」が解けないことを証明するのは比較的簡単です。
「14-15パズル」では、図1のゴールから14のパネルと15のパネルが置き換わっただけの状態ですので、1次元配列Sは以下のようになります。
S = {1,2,3,4,5,6,7,8,9,10,11,12,13,15,14,空}
以下、実際に説明通りパネルを動かすことができませんが、空と数字パネルの交換方式で最短経路を示せば、以下のようになります。
14と15のパネルを入れ替えるために、まず空と15を入れ替えます。
S1 = {1,2,3,4,5,6,7,8,9,10,11,12,13,空,14,15}
その後、空と14を入れ替え、
S2 = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,空,15}
そして、空と15を入れ替えるのが最短の入れ替えによるゴールへの到達となります。
S3 = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,空}
初期状態の1次元配列Sからゴールの1次元配列S3まで置換回数は3回ですが、「空」は動きませんので、
『パネルの置換回数と「空」を動かす回数を加えると偶数になる』という法則に反しているためこのゴールへは到達できないということがわかります。
簡単のため、最短経路で説明しましたが、最短経路でなくても結果は同じです。
これを示すため、空と15を直接入れ替えるのではなく、Sと同じ状態の1次元配列Pから、15とある数字パネルAとの交換を経由してS1と同じ状態P3へ持ってゆくことを考えると、
以下の通り、どうしても置換回数は3回になってしまいますし、どんな複雑なパネル交換を経由しても置換回数は2回づつ増えて行きます。
したがって、どんな複雑なパネル交換を経由してもゴールへは到達できないという結論が変わることはありません。
P = {・・・,A,・・・,15,14,空}
P1 = {・・・,15,・・・,A,14,空}
P2 = {・・・,空,・・・,A,14,15}
P3 = {・・・,A,・・・,空,14,15}
15パズルを速く解くためのヒント
前節の「パネルを動かした時の1次元配列の変化」から15パズルを速く解くためのヒントも得られます。
即ち、パネルを横に動かす操作は「空」と横のパネル数字との入れ替えでしかないため、
図6に示す通り最後に一行だけ残すと、その上の行まで崩さないとゴールには到達できなくなってしまい無駄な時間が発生します。
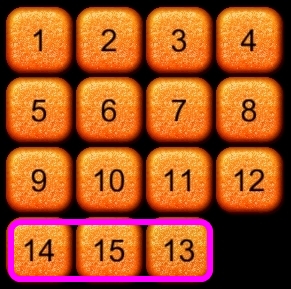
図6 最後の一行が残ったケース
そして、下二行になったら、図7に示す通り、左側から9と13、その次が10と14を揃えて行けば、自ずとゴールに速く辿り着けることがわかります。
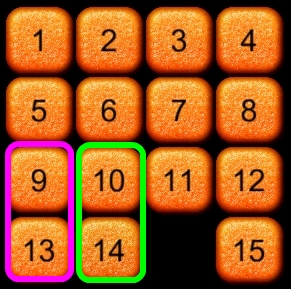
図7 下二行の解き方








-172.31.37.45。